14_Активные фильтры АТСб-23-1
Проработать до 17.12.2025, ответить на вопросы, законспектировать
Основные теоретические сведения
Одной из важных операций в электронных устройствах является выделение полезного сигнала по частотному признаку. Эта операция носит название частотной селекции, частотной избирательности или фильтрации. Устройства, осуществляющие эту операцию, называются частотными фильтрами или просто фильтрами.
Различают фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ) и др. Рассмотрим свойства ФНЧ. Основное свойство ФНЧ – с минимальным ослаблением передавать на выход колебания, частоты которых меньше заданной граничной частоты, называемой частотой среза фильтра fср. В то же время колебания с более высокими частотами должны существенно ослабляться. Идеальная частотная зависимость коэффициента передачи мощности Кпер.Р фильтра с частотой среза fср изображена на рис. 1 штриховой линией.
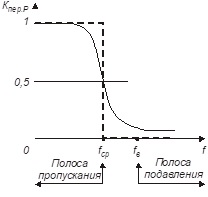
Рисунок 1 - Частотная характеристика ФНЧ
Такая частотная характеристика физически заведомо нереализуема. Реальная частотная характеристика – сплошная линия на рис. 1 – имеет неравномерность коэффициента передачи в полосе пропускания и переходный участок от полосы пропускания к полосе подавления. Началом полосы подавления принято считать частоту fв, коэффициент передачи на которой на +3 дБ по напряжению больше, чем в полосе подавления на частотах, много больших частоты среза.
Имеется несколько способов подбора допустимой аппроксимирующей функции для идеальной частотной характеристики.
Один из возможных способов аппроксимации идеальной характеристики ФНЧ построен на использовании коэффициента передачи мощности по зависимости:
![]()
где s=f / fср – безразмерная нормированная частота.
ФНЧ, имеющий такие частотные свойства, называется фильтром с максимально-плоской характеристикой или фильтром Баттерворта. Целое число n=1, 2, 3, … является порядком фильтра. В полосе пропускания фильтра, т.е. при 0≤s≤1, квадрат модуля коэффициента передачи плавно уменьшается с ростом частоты. На частоте среза (при s=1) ослабление по мощности, вносимое фильтром, составляет примерно 2 раза независимо от порядка фильтра. Чем больше n, тем точнее аппроксимация идеальной формы характеристики. На рис. 2 в линейном масштабе изображены графики, построенные для максимально-плоских характеристик фильтров различных порядков.
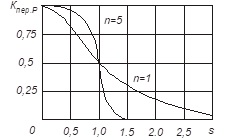
Рисунок 2 - Частотные характеристики коэффициента передачи мощности для ФНЧ типа Баттерворта при n=1 и n = 5
Широко применяется также другой способ аппроксимации, получивший название чебышевской аппроксимации. В фильтре Чебышева имеются волнообразные зубцы на графике коэффициента передачи в полосе пропускания, и характеристика равномерна в полосе подавления.
